ミカエリス・メンテンの式とは、酵素反応の初速度を表すものです。
酵素反応の反応機構を調べることは、酵素の果たす役割を考えると重要な課題となっています。そのために化学反応速度論をを用いることは有効なアプローチのうちの1つと言えます。
今回は反応速度論からミカエリスメンテンの式を導出し、実際の実験データから反応初速度を反応物の濃度に対してプロットします。
目次
ミカエリス・メンテン式の導出
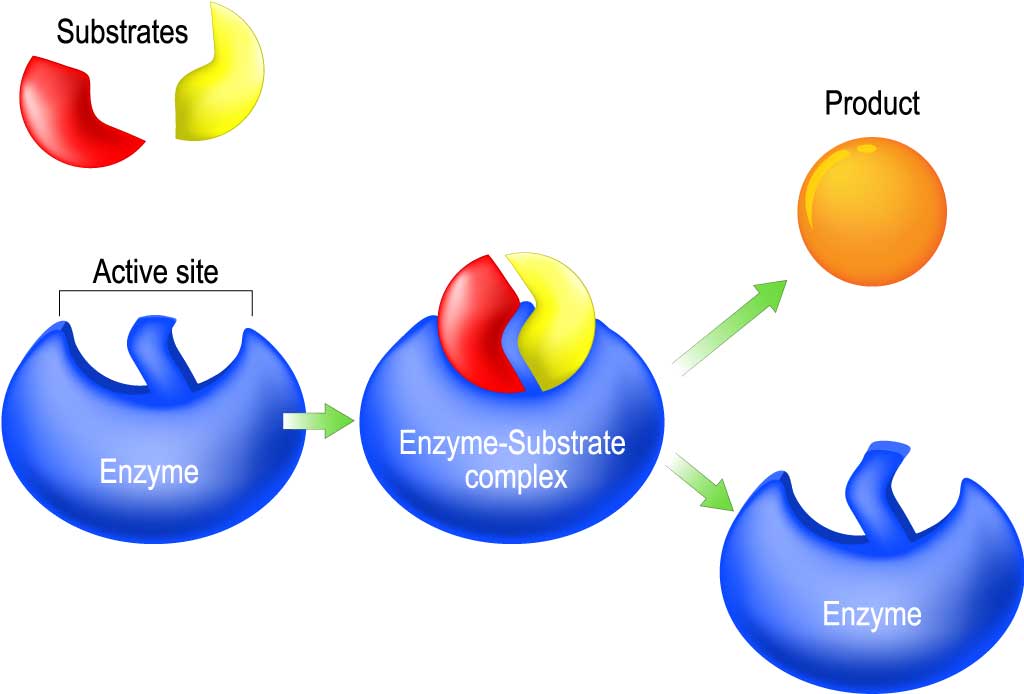
最も単純な酵素反応は、1つ基質が酵素と複合体をつくり、それが生成物と酵素に分解するモデルを考えることができます。

Eは酵素(enzyme)、Sは基質(substrate)、ESは酵素-基質複合体(enzyme-substrate complex)、Pは生成物(product)です。
この反応は基質の濃度が酵素に比べて十分高ければ全ての酵素がESの形になっているため、Pの生成速度は2つ目の反応によって決まり、これが律速段階となるわけです。
したがって酵素の濃度を一定として、基質の濃度を増やしていってもいつか頭打ちになります。この仮定のもと、この反応の反応速度は、
また、ESの正味の生成速度は、
ミカエリス・メンテンの式を求めるための2つの仮定
(2)式の微分方程式を[ES]について解いて反応速度式に代入し、反応速度を求めるのは無理なので次の2つの仮定をおくことで式を簡単にします。
- 第一段階反応は平衡状態にあるとする。
- 反応開始直後のごく初期(数ms)を除くと、基質濃度は酵素よりも十分高いと考えてよく、全ての酵素がESの形であるとする。つまり、[ES]の正味の生成速度はゼロである。この状態のことを定常状態と呼びます。
反応速度を求めるために[ES]について解く
(2)式と(3)式の右辺をイコールでつなげて、
また、酵素の全濃度を\([E]_t\)とおけば、
(5)式を(4)式に代入して\([E]\)を消去、
これを式変形して\([ES]\)についてまとめると、
両辺を\(k_1\)で割ると、
\([ES]\)について解けば、
ここで、ミカエリス定数
をおくと(6)式は
になる。
いわゆる反応初速度とは一体いつの速度のことなのか
それでは、反応開始直後(t=0~数ミリ秒)の(3)式が成立するまでの時間を除いた反応の初期のことを考えてみましょう。
この時間帯は酵素の不活性化や生成物による反応の阻害がないため、反応速度は(1)式に従います。
そのときの反応速度を反応の初速度\(v_0\)として考えれば、(1)式と(8)式より、
ただし、反応開始からある程度時間が経つと生成物が増えて反応を阻害したり基質の量が少なくなって仮定2が成立しなくなるため反応速度が落ちてしまいます。
ミカエリス・メンテンの式
反応の初期において、酵素濃度一定のもと基質濃度が十分高く酵素が基質で飽和し、全ての酵素が酵素-基質複合体になったときの速度が反応初速度の最大値となりますので、最大速度\(V_{max}\)は、
(10)式を(9)式に代入すれば、
これがミカエリス・メンテンの式です。
反応初速度を基質濃度に対してプロットしてみる。
実際の実験から得られたデータを用いて、酵素反応の初速度を基質濃度に対してプロットしてみましょう。プロットとは点を打つという意味です。
前提
乳酸脱水素酵素(LDH)は以下の反応を触媒します。
ピルビン酸 + NADH + H+ ⇄ L-乳酸 + NAD+
このとき、NADHは340 nmに吸収波長をもつがNAD+はもたないため、分光光度計を用いて吸光度の時間変化を追うことでLDHの活性測定を行うことができます。そしてLDHはミカエリス・メンテンの式に従うこともわかっています。
内容と結果
今回の実験では反応溶液中のLDH濃度を0.014 mg/mLに固定し、複数のピルビン酸濃度条件に対してNADHの吸光度の時間変化を測定しました。
得られた吸光度の時間変化のデータから各濃度条件における反応初速度を計算し、ピルビン酸濃度に対してプロットしたものを下の図に示します。

反応初速度と基質の関係 ピルビン酸の濃度が高くなるにつれて反応初速度がだんだん横ばいになっていくのがわかります。ピルビン酸の濃度を限りなく大きくしたときの極限値が反応の最大速度になります。
また、(9)式に\([S]=K_M\)を代入すると\(v_0=\frac{V_{max}}{2}\)です。
従って、グラフから\(V_{max}\)を推測し、曲線において反応初速度が\(\frac{V_{max}}{2}\)のときのピルビン酸濃度の値が\(K_M\)になります。ただし、あまり正確な値は出せないでしょう。
より正確な最大速度とミカエリス定数を求めるためにはラインウィーバー・バークプロットやイーディー・ホフステープロットを用いた方が良いでしょう。