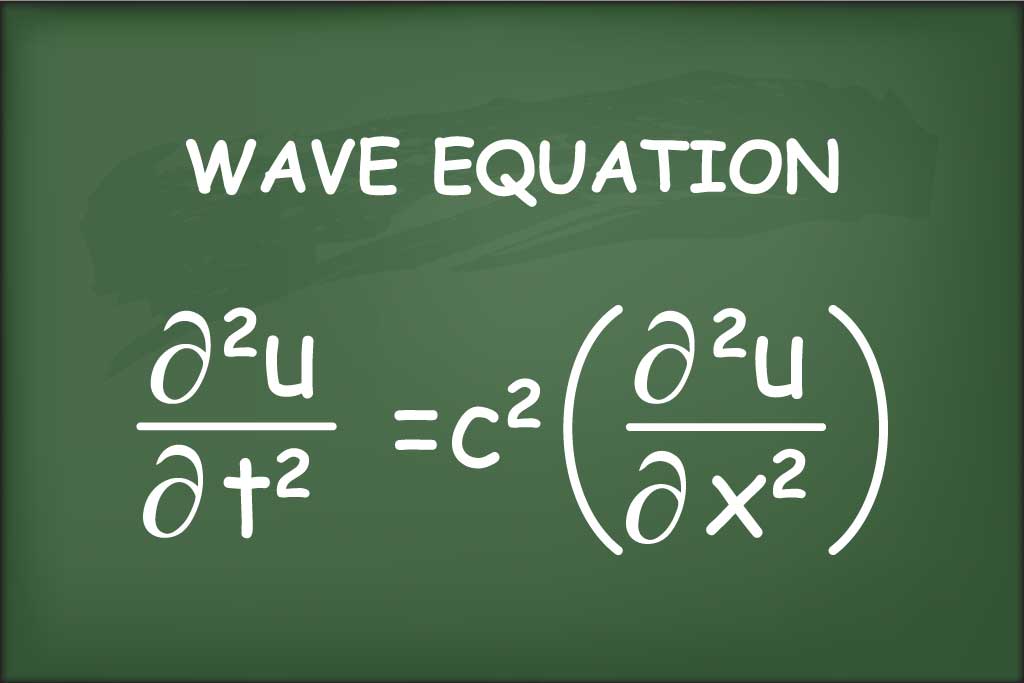古典的な波動方程式の解き方

古典的波動方程式は、量子力学でおなじみのシュレディンガー方程式を理解するうえでの基礎になります。今回は、一次元の波動方程式を解いていきます。

1 振動する弦の波動方程式
2 波動方程式は変数分離法を使って解くことができる
3 波動の変位u(x,t)を求める
- 3.1 分離定数K>0のときの変位u(x,t)
- 3.2 分離定数K<0のときの変位u(x,t)

振動する弦の波動方程式

まず、両端が固定された弦を振動させたときの弦の振る舞いを考えます。

上図のように、左端を原点として、時刻$t$における位置$x$の変位を$u(x,t)$とします。端点間の長さは$l$とします。このとき、$u(x,t)$は以下の方程式を満足することが知られています。これを古典的波動方程式といいます。

$$\frac{\partial^2 u(x,t)}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 u(x,t)}{\partial t^2} \tag{1}$$

このとき、$v$は弦を伝わる波の速度になります。今回は、この方程式を既知のものとして解き進めていきます。

さて、上図の弦は両端が固定端になっているため、時刻$t$によらず変位は$0$になります。このように、$u(x,t)$が満たすべき条件のことを境界条件と呼びます。式に表すと以下のようになります。

$$u(0,t)=u(l,t)=0 \tag{2}$$

波動方程式は変数分離法を使って解くことができる

波動方程式は、偏微分方程式の解法の１つである変数分離法によって解くことができます。変数分離法では、２変数関数である$u(x,t)$が2つの１変数関数$X(x)$と$T(t)$の積であると仮定します。

$$u(x,t)=X(x)T(t) \tag{3}$$

変数分離法で仮定した(3)式を波動方程式(1)に代入します。

$$\frac{\partial^2 \{X(x)T(t)\}}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \{X(x)T(t)\}}{\partial t^2} $$

偏微分に関係ない関数は外に出して、

$$T(t)\frac{d^2 X(x)}{d x^2}=\frac{1}{v^2}X(x)\frac{d^2 T(t)}{d t^2} $$

このとき、方程式の微分の部分が１変数関数の微分、すなわち常微分に変わったので微分記号が$\partial{}$から$d$になっています。

両辺を$u(x,t)=X(x)T(t)$で割ると、

$$\frac{1}{X(x)}\frac{d^2 X(x)}{d x^2}=\frac{1}{v^2T(t)}\frac{d^2 T(t)}{d t^2} \tag{4}$$

上の(4)式では、左辺の変数が$x$のみで、右辺の変数は$t$のみになっています。xとtは互いに独立な変数ですから、(4)式が任意の$x$および$t$で成り立つためには(左辺)=(右辺)=(定数)が必要です。したがって、定数を$K$などとおけば(4)式は、

$$\frac{1}{X(x)}\frac{d^2 X(x)}{d x^2}=\frac{1}{v^2T(t)}\frac{d^2 T(t)}{d t^2} =K$$

すなわち、

$$\begin{align} \frac{1}{X(x)}\frac{d^2 X(x)}{d x^2}&=K \tag{5} \\ \frac{1}{v^2T(t)}\frac{d^2 T(t)}{d t^2} &=K \end{align} \tag{6}$$

となります。このとき、定数としておいた$K$を分離定数と呼び、実際の値は波動方程式を解く過程で求まります。

(5)(6)式を変形して整理すれば、

$$\begin{align} \frac{d^2 X(x)}{d x^2}-KX(x)&=0 \tag{7} \\ \frac{d^2 T(t)}{d t^2}-Kv^2T(t) &=0 \end{align} \tag{8}$$

上の(7)(8)式はいずれも１変数関数の微分方程式であるため、常微分方程式になります。また、変数とその微分が１乗の形でしか現れていないことと、方程式の各項の係数が定数であることから、(7)(8)式は定係数の線形微分方程式でもあります。このような方程式は簡単に解くことができます。具体的には、$K$の値が０か正か負かで場合分けします。

分離定数K=0のとき

まずは$K=0$の場合を仮定します。$K=0$を(7)(8)式に代入して、

$$\begin{align} \frac{d^2 X(x)}{d x^2}&=0 \\ \frac{d^2 T(t)}{d t^2} &=0 \end{align} $$

$X(x)$と$T(t)$を２階微分するといずれも０になるわけですから、解は、

$$\begin{align} X(x)&=a_1x+b_1 \\ T(t)&=a_2t+b_2 \end{align} $$

ただし、$a$と$b$は積分定数です。確かに、上の２式を２階微分すれいずれも$０$になります。

これと、(2)式の境界条件、

$$u(0,t)=u(l,t)=0 \tag{2}$$

より、

$$u(0,t)=X(0)T(t)=(a_1 \cdot 0+b_1)(a_2t+b_2)=0 $$

$$u(l,t)=X(l)T(t)=(a_1l+b_1)(a_2t+b_2)=0$$

ここで、弦の変位$u(x,t)$は時間変化するため、つねに$T(t)=0$となることはありません。上２式がtの値に関わらず成り立つためには$X(0)=X(l)=0$、すなわち$a_1=b_1=0$であることが必要です。このとき、

$$X(x)=a_1x+b_1=0 \cdot x+0=0$$

$$u(x,t)=X(x)T(t)=0 \cdot T(t)=0　\tag{9}$$

になります。これは、弦の変位が時間と位置に関係なく$0$になってしまうため物理的に意味のない解です。このような解を無意味な解と呼びます。

分離定数K>0のとき

次に、分離定数$K>0$のときです。改めて、(7)(8)式を以下に示します。

$$\begin{align} \frac{d^2 X(x)}{d x^2}-KX(x)&=0 \tag{7} \\ \frac{d^2 T(t)}{d t^2}-Kv^2T(t) &=0 \end{align} \tag{8}$$

上の２式はいずれも、

$$\frac{d^2y}{dx^2}-k^2y(x)=0　\tag{9}$$

の形で表される方程式であることがわかります。このとき、$k$は実数定数であるとします。$K=0$のときに述べましたが、このタイプの方程式は定係数の線形微分方程式と呼ばれ、解はいつも$y=\mathrm{e}^{αx}$ の形をとることがわかっています。$α$は定数で、方程式を解く過程で決まります。

$ y= \mathrm{e}^{αx}$ を(9)式に代入して、

$$\frac{d^2}{dx^2}\mathrm{e}^{αx}-k^2\mathrm{e}^{αx}=0$$

左辺第１項の２階微分を計算して、

$$α^{\:2} \: \mathrm{e}^{αx}-k^2 \: \mathrm{e}^{αx}=0$$

共通因数で括って、

$$(α^{\:2}-k^2 \: )\mathrm{e}^{αx}=0$$

よって、

$$α^{\:2}-k^2=0　\mathrm{または}　\mathrm{e}^{αx}=0$$

$\mathrm{e}^{αx}=0$のときは$y(x)=0$で無意味な解となるため、$α^{\:2}-k^2=0$です。これを解いて、

$$α=\pm k$$

したがって、(9)式の解は

$$\begin{align} y(x)&=\mathrm{e}^{\,kx} \\ y(x)&=\mathrm{e}^{\:-kx} \end{align} $$

であり、一般解を求めると、

$$y(x)=c_1\mathrm{e}^{\,kx}+c_2\mathrm{e}^{\:-kx}　\tag{10}$$

になります。ただし、$c_1$と$c_2$はともに定数です。定係数の線形微分方程式の解き方について詳しく知りたい方は常微分方程式の教科書を参照してください。

直感的な理解としては、得られた2つの解の線形和もまた方程式の解であり、２階微分を含む方程式を解くためには積分を２回実行する必要があることから、(10)式のように定数が2つ現れることになります。

あとは(7)(8)式に応じて$k$の値を決定すれば良いですし、境界条件などを利用すれば定数cの値も求まります。

分離定数K<0のとき

最後に、分離定数$K<0$のときです。解き方の流れは$K>0$のときと同じです。再度、(7)(8)式を以下に示します。

$$\begin{align} \frac{d^2 X(x)}{d x^2}-KX(x)&=0 \tag{7} \\ \frac{d^2 T(t)}{d t^2}-Kv^2T(t) &=0 \end{align} \tag{8}$$

$K<0$を仮定したことから上２式の左辺第２項目の係数は正になるので、両式ともに、

$$\frac{d^2y}{dx^2}+k^2y(x)=0　\tag{11}$$

の形で表すことができます。$k$は実数定数です。これは定係数の線形微分方程式であるため、$ y= \mathrm{e}^{αx}$ を解にもちます。これを(11)式に代入して、

$$\frac{d^2}{dx^2}\mathrm{e}^{αx}+k^2 \: \mathrm{e}^{αx}=0$$

式を整理して、

$$(α^{\:2}+k^2 \: )\mathrm{e}^{αx}=0$$

よって、

$$α^{\:2}+k^2=0　\mathrm{または}　\mathrm{e}^{αx}=0$$

$\mathrm{e}^{αx}=0$のときは$y(x)=0$で無意味な解となるため、$α^{\:2}+k^2=0$です。これを解いて、

$$α=\pm \mathrm{i}k$$

したがって、(9)式の解は、

$$\begin{align} y(x)&=\mathrm{e}^{\,\mathrm{i}kx} \\ y(x)&=\mathrm{e}^{\:-\mathrm{i}kx} \end{align} $$

であり、一般解を求めると、

$$y(x)=c_1\mathrm{e}^{\,\mathrm{i}kx}+c_2\mathrm{e}^{\:-\mathrm{i}kx} \tag{12}$$

このとき、($c_1$と$c_2$はともに定数です。$K>0$のときと比較すると、$α$の値が$\pm k$から$\pm \mathrm{i}k$に変わっただけなのがわかります。さて、$\mathrm{e}$を底とする指数関数の指数部分が虚数になった際には、以下に示すオイラーの式と呼ばれる式を用いて式を書き換えることができます。

$$ e^{\pm \mathrm{i}\theta} = \cos\theta \pm \mathrm{i}\sin\theta $$

$\theta=kx$のときのオイラーの式を(12)式に代入して、

$$\begin{align} y(x)&=c_1(\cos{kx}+\mathrm{i}\sin{kx})+c_2(\cos{kx}-\mathrm{i}\sin{kx}) \\ &=(c_1+c_2)\cos{kx}+ (\mathrm{i}c_1-\mathrm{i}c_2)\sin{kx}\end{align}$$

になりました。このとき、$c_1+c_2$および$\mathrm{i}c_1-\mathrm{i}c_2$は定数であるので、それぞれ$c_3$と$c_4$に置き換えて見やすくします。

$$y(x)=c_3\cos{kx}+c_4\sin{kx} \tag{13}$$

以上、$K$の範囲で場合分けして方程式を解くことによって、$u(x,t)=X(x)T(t)$の$X(t)$と$T(t)$がどのような式になるのかを文字定数を用いて表すことができました。

次の項からは、$X(x)$と$T(t)$をそれぞれ具体的に求めて$u(x,t)$を決定します。

波動の変位u(x,t)を求める

ここまでは、古典的な波動方程式を、変数分法を用いながら分離定数$K$の範囲で場合分けをすることで解き進めてきました。ここからは、求められた関数$u(x,t)$の文字定数の部分を決定していきます。以下は、(7)(8)式の再掲です。

$$\begin{align} \frac{d^2 X(x)}{d x^2}-KX(x)&=0 \tag{7} \\ \frac{d^2 T(t)}{d t^2}-Kv^2T(t) &=0 \end{align} \tag{8}$$

$K=0$のときは無意味な解になるため考えません。

分離定数K>0のときの変位u(x,t)

$K>0$のとき、$K=β^{\:2}$を満たす実数$β$をおきます。先の議論で、$K>0$のときの$X(x)$と$T(t)$が(10)式の形で表されることがわかりました。

$$y(x)=c_1\mathrm{e}^{\:kx}+c_2\mathrm{e}^{\:-kx}　\tag{10}$$

その過程で、(7)式から(9)式に移るところで$K=k^2$とおいていたため、これを満たす$k$を$\beta$とおいて(10)式に$k=\beta$を代入すれば(7)式は、

$$X(x)=c_1\mathrm{e}^{\:\beta x}+c_2\mathrm{e}^{\:-\beta x}$$

これと(2)式の、

$$u(0,t)=u(l,t)=0 \tag{2}$$

より、$x=0,l$における変位$u$は時刻$t$によらず$0$であるため、$X(0)=X(l)=0$ですから、

$$X(0)=c_1+c_2=0$$

$$X(l)=c_1\mathrm{e}^{\:\beta l}+c_2\mathrm{e}^{\:-\beta l}=0$$

この連立方程式を$c_1$と$c_2$について解くと$c_1=c_2=0$になりますが、$X(x)=0$になっていしまいます。よって、$u(x,t)=0$となり、分離定数$K>0$のときも方程式の解は無意味です。残るは$K<0$のときです。

分離定数K<0のときの変位u(x,t)

最後に、分離定数$K<0$のときです。流れは$K>0$のときと同じです。先の議論で、$K<0$のときの$X(x)$と$T(t)$が(13)式の形で表されることがわかりました。

$$y(x)=c_3\cos{kx}+c_4\sin{kx} \tag{13}$$

その過程で、(7)式から(11)式に移るところで$K=-k^2$とおいていたため、これを満たす$k$を$\beta$とおいて(13)式に$k=\beta$を代入すれば(7)式は、

$$X(x)=c_3\cos{\beta x}+c_4\sin{\beta x} \tag{14}$$

これと境界条件の(2)式、

$$u(0,t)=u(l,t)=0 \tag{2}$$

より、$x=0,l$における変位$u$は時刻$t$によらず$0$であるため、$X(0)=X(l)=0$ですから、

$$X(0)=c_3\cos{(\beta \cdot 0)}+c_4\sin{(\beta \cdot 0)} =0$$

$$X(0)=c_3\cos{\beta l}+c_4\sin{\beta l} =0$$

１つ目の式より$C_3=0$で、これと２つ目の式より、

$$c_4=0　または　\sin{\beta l}=0 $$

$c_4=0$のとき、$X(x)=0$より$u(x,t)=0$ですから、このときの解は無意味なものになります。$\sin{\beta l}=0 $のときだと、

$$\beta l=nπ　(n=1,2,3,…) \tag{15}$$

これと$c_3=0$を(14)式に代入して$\beta$を消去すれば、

$$X(x)=c_4\sin{\frac{nπx}{l}} \tag{16}$$

(8)式も解きます。$T(t)$の解も$X(t)$と同じく(13)式の形で表されますが、定数$k$の重複を避けるために$k_1$とします。

$$y(x)=c_3\cos{k_1x}+c_4\sin{k_1x} \tag{13}$$

$$\frac{d^2y}{dx^2}+{k_1}^2y(x)=0　\tag{11}$$

(8)式から(11)式に移る際に$Kv^2=-{k_1}^2$とおくことから、${k_1}^2=\beta^2 v^2$の関係を得ます。したがって、(8)式は、

$$T(t)=c_5\cos{βvt}+c_6\sin{βvt} $$

このとき、係数$c$についても重複を避けるため、$X(t)$の係数とは別の文字$c_5,c_6$を用いました。これに(16)式を代入して$\beta$を消去すれば、

$$T(t)=c_5\cos{\frac{nπvt}{l}}+c_6\sin{\frac{nπvt}{l}} \tag{17}$$

(16)(17)式より、

$$\begin{align} u(x,t) &=X(x)T(t) \\ &=c_4\sin{\frac{nπx}{l}}\:\:(c_5\cos{\frac{nπvt}{l}}+c_6\sin{\frac{nπvt}{l}}\:\:) \\ &=(B\cos{\frac{nπvt}{l}}+C\sin{\frac{nπvt}{l}}\:\:)\sin{\frac{nπx}{l}} \end{align} $$

ここで、簡素化のために$c_4c_5=B$、$c_4c_6=C$とおきました。また、$u(x,t)$は自然数$n$にも依存しているので、

$$u_{\:n}(x,t)=(B_n\cos{\frac{nπvt}{l}}+C_n\sin{\frac{nπvt}{l}}\:\:)\sin{\frac{nπx}{l}} \tag{18}$$

と表し直します。このことから、変位$u$は複数の解をもつことになるわけですが、そもそもの始まりである波動方程式(1)が線形微分方程式であるため、一般解は(18)式の無限間数列の和になるわけです。よって、一般解は、

$$\begin{align} u(x,t) &=\sum_{n=1}^{\infty} u_{\:n}(x,t) \\ &=\sum_{n=1}^{\infty}(B_n\cos{\frac{nπvt}{l}}+C_n\sin{\frac{nπvt}{l}}\:\:)\sin{\frac{nπx}{l}} \end{align}$$

三角関数の合成により、上式の( )内は$A_n\cos{(\frac{nπvt}{l}+φ_n)}$の形で表されるので、

$$u(x,t)=\sum_{n=1}^{\infty}A_n\cos{(\frac{nπvt}{l}+\phi_n)}\sin{\frac{nπx}{l}} \tag{19}$$

これが古典的な波動方程式の解です。